Задания по математике конкурса
«Этот прекрасный удивительный и загадочный мир»
5 класс
Задание №1: Ученик должен написать математическое сочинение на заданную тему, в котором он должен дать решение и объяснение поставленных в математическом эссе проблем познания (выделены жирным шрифтом).
Родственные связи
Родина, мать и отец, семья – с этого начинается для каждого отчизна. Ради свободы и благополучия отчизны люди никогда не жалели ни сил, ни жизни. Это воспето в песнях и запечатлено в душах патриотов. А так ли мы хорошо знаем свою родину? Да хотя бы свою семью?… Кто знает из вас кто такой «деверь»? А кто такая «падчерица»? То-то! Семьей надо не только быть, надо знать всё о своей семье, а иначе, в какой-то момент из-за вас же возникшей неловкости в отношениях между близкими людьми можно будет иметь бледный вид…
Замечательное дело – большие счастливые семьи – оазисы добра и счастья! Чем больше семья – тем больше проблем, тем мудрее должны быть все члены семьи – от мала до велика. Только тогда эти оазисы доброты и благополучия не погибнут.
На семейном совете было обнаружено, что среди присутствующих имеются следующие люди: отец, мать, сын, дочь, тетя, дядя, брат, сестра, двоюродная сестра, двоюродный брат, племянник, племянница. Но там было всего четыре человека. Как такое могло быть?
Подъехали опоздавшие на совет муж с женою, брат с сестрою да кум с кумой. Сколько всего человек прибыло на семейный совет?
Мудрость возрасту не помеха. Поэтому решите следующие, то ли головоломки, то ли обычные жизненные проблемы, накопившиеся за годы совместной жизни и нахлынувшие вдруг. Подключитесь к семейному совету и покажите, как можно найти решение даже самых хитроумных сплетений человеческих судеб и местных обычаев.
Проблема первая: Сын – дед самому себе. Если это возможно, то как?
Проблема вторая: Бывают ли трехлетние дедушки?
Проблема третья: У семерых братьев по одной сестрице. Много ли всех сестриц?
Проблема четвертая: Сын отца моего, а мне не брат?
Проблема пятая: Как выйти замуж за брата своего вдовца?
Семейный уклад – многовековой уклад, семейные традиции и мораль – нить семейных ценностей, протянувшаяся через века от предков к нам.
Отношения дедов и внуков трогательны – одни начинают свой жизненный путь, а другие его завершают. Различия во взглядах на жизнь столь велики, что кажутся порой непреодолимы. Но это только кажется… Что точно непреодолимо так это разница в возрасте, которая порождает порой любопытные коллизии. Вот некоторые из них:
Коллизия первая: Сколько дедушке лет, столько месяцев внучке. Вместе им 91 год. Сколько лет дедушке и сколько внучке?
Коллизия вторая: Деду, отцу и сыну вместе 100 лет. Отцу и сыну вместе 45 лет. Сын на 25 лет моложе отца. Сколько кому лет?
Коллизия третья: Деду 64 года, внуку 16 лет. Через сколько лет дед станет втрое старше внука?

Семейное древо велико и ветвисто. Далеко в прошлое уходят его корни и в заоблачные дали смотрят его ветви. Всех родственников наших по отцовской и материнской линии считать - не пересчитать – имя им «легион». Хотя можно с этим и не согласиться. Сколько всего прабабушек и прадедушек было у всех ваших прабабушек и прадедушек?
Проблемы можно найти, и, не заглядывая столь далеко и столь глубоко, а поблизости – практически на поверхности.
Брат – старшеклассник спросил у сестренки: «Сколько дней тебе было ровно в три раза меньше лет, чем мне?». «Три дня», - ответила сестра. «А в 4 раза?» - «4 дня.» - «А в 6 раз?». Тут сестренка задумалась. Она знала, что такие дни были, но сколько? Помогите ей ответить.
Проблемы возникают не сразу - они вырастают, вместе с людьми. Позавчера Пете было 17 лет. В следующем году ему будет 20 лет. Как такое может быть?
Только окунувшись в семейные проблемы, понимаешь, насколько обширны они и глубоки. Кто-то тратит на распутывание семейных проблем всю свою жизнь, забывая, что жизнь не для этого, а для жизни наполненной любви и счастья. Но, если пришла беда – отворяй ворота! И встречай беду во всеоружии, чтобы сохранить данный тебе на попечение человеческий островок счастья. Берегите друг друга!
Задание №2: Заполните пустые клетки цифрами от 1 до 9, но так, чтобы в любой строке по горизонтали и по вертикали и в каждом из девяти блоков, отделенных жирными линиями, не было двух одинаковых цифр. Желаем удачи!

6 класс
Задание №1: Ученик должен написать математическое сочинение на заданную тему, в котором он должен дать решение и объяснение поставленных в математическом эссе проблем познания (выделены жирным шрифтом).
Землекопы прошлого и настоящего
Философия землекопа проста и честна: «Копай глубже. Кидай дальше. Пока летит – отдыхаешь…» Этой философии несколько десятков тысяч лет, она родилась в тот момент, когда наш предок взял в руку палку-копалку. С тех пор, если она и изменялась, то несущественно, в той мере, в какой менялось орудие землекопа.



Многие века орудие труда землекопа – лопата. Инструмент, который состоит из полотна, вилки, ручки, стержня, ребра жёсткости и тупейки. Несмотря на простоту орудия, землекопы орудуют им виртуозно. Лопаты делятся на следующие виды: саперная, штыковая, совковая и т. д.
Руки заняты – зато голова свободна. Есть о чем поразмыслить во время работы, благо жизнь всегда подкидывает задачки. Три землекопа за 2 часа вырыли 3 ямы. Сколько ям выроют 6 землекопов за 5 часов?
А если на ситуацию взглянуть по-другому. Мало ли какие запросы у заказчика? Всё сделаем как вы просите за ваши деньги… Три землекопа могут вырыть траншею ровно за один день. Сколько нужно землекопов, чтобы вырыть такую же траншею ровно за два дня?
Землекопы, несмотря на орудие труда, которое выглядит примитивно, сами-то лыком не шиты. Если двенадцать человек, работая по восемь часов в день, должны выкопать яму глубиной в десять с половиной миль, сколько времени пройдет – считая и воскресные дни! – прежде чем они положат лопаты?
Не все члены бригады землекопов могут похвастаться трудолюбием или просто любовью к своей профессии. Труд-то тяжелый, да и малоквалифицированный – повод для гордости небольшой.
Бригада из 6 землекопов в течение 8 часов копала канаву. При этом в каждый момент времени работало ровно двое, а остальные играли в карты. В конце рабочего дня оказалось, что первый землекоп играл в карты 3 часа, второй – 4 часа, третий – 5 часов и пятый – 7 часов. Сколько часов играл в карты шестой землекоп?
Приведем в качестве примера ещё один случай безответственного отношения к делу. Трое рабочих копали канаву. Сначала первый рабочий проработал половину времени, необходимого двум другим, чтобы вырыть всю канаву, затем второй проработал половину времени, необходимого двум другим, чтобы всю канаву, и, наконец, третий проработал половину времени, необходимого двум другим, чтобы вырыть всю канаву. В результате канава была вырыта. Во сколько раз быстрее была бы вырыта канава, если бы с самого начала работали все трое рабочих одновременно?
Поэтому хочешь добиться хорошего результата за приемлемые деньги – научись их считать. Курочка по зернышку клюет, а какая вырастает?... Для рытья канавы были наняты два землекопа. Один из них может за час прокопать в два раза больше, чем другой, а платят за каждый час работы одинаково. Что обойдется дешевле: если землекопы будут рыть канаву одновременно с двух сторон или если каждый из них выроет половину канавы?
Экономить на зарплате для землекопов вряд ли удастся – себе дороже будет. Что-что, а деньги землекопы считать умеют. Зарплата дорожной работницы — 6 рублей в день. Ежедневно бригада из 5 дорожных работниц роет по 15 метров канавы. Сколько метров канавы должна вырыть эта бригада, чтобы заработать столько же, сколько зарабатывает за один вечер группа риска из 5 девушек, если каждая девушка получает за вечер, проведённый в интуристовской гостинице, 100 долларов, а один доллар по курсу чёрного рынка равен 50 рублям?
За тяжелый труд платить гроши тоже аморально, а на женском труде наживаться, вообще, преступление, поэтому все упреки в некорректности сравнения в предыдущей задаче отвергаем сходу. Любой труд у нас в почёте. Или вы с чем-то не согласны?

Теперь землекопа можно чаще всего встретить за рулем экскаватора. Увеличились объемы перемещаемого грунта, но характер, как и философия труда, изменились мало: «Бери больше. Кидай дальше…» От этого труд не стал менее востребован – наоборот, получив в руки лопату, в которую помещается полтонны земли и более, можно горы свернуть и реки вспять повернуть. Планов громадьё человечества распространилось на Вселенную. В ближайшее время начнется освоение Луны, и кто будет там востребован более всего? Угадайте с трёх раз!
Задание №2: Заполните пустые клетки цифрами от 1 до 9, но так, чтобы в любой строке по горизонтали и по вертикали и в каждом из девяти блоков, отделенных жирными линиями, не было двух одинаковых цифр. Желаем удачи!
7 класс
Задание №1: Ученик должен написать математическое сочинение на заданную тему, в котором он должен дать решение и объяснение поставленных в математическом эссе проблем познания (выделены жирным шрифтом).
Мудрецы всех времен и народов
Мудрецы всегда были в почете. Без них в трудную минуту никак не обойтись. Свой ум они совершенствовали в спорах и разгадках различных головоломок и житейских проблем.



Как-то утомившись от споров и летнего зноя, три древнегреческих мудреца прилегли отдохнуть и уснули. Пока они спали, шутники испачкали углем их лбы. Проснувшись, и взглянув друг на друга, они начали смеяться, так как каждый полагал, что двое других смеются друг над другом. Внезапно один из мудрецов перестал смеяться, так как он сообразил, что его собственный лоб также запачкан. Как он рассуждал?
Мудрецы тоже люди и им не чужды человеческие слабости и ошибки, но в отличие от простаков они всегда могут найти выход из сложившейся ситуации.
Мудрец, увлекающийся алхимией, хранит эликсир в четырех одинаковых сосудах. Можно сливать два сосуда в один (сосуд может вместить весь эликсир), или поставить два сосуда на чашечные весы, и лить из третьего в тот, где эликсира меньше, пока весы не уравновесятся (или эликсир в третьем сосуде не кончится). Алхимик помнит, что так можно получить сосуд ровно с одной унцией эликсира, но не помнит, как. В каждом сосуде целое число унций эликсира. Один из сосудов пуст. Докажите, что можно, попереливав, восстановить исходные количества в каждом сосуде и при этом узнать, где сколько эликсира.
Где мудрецам почерпнуть мудрости? - только у таких же мудрецов! Поэтому и собираются мудрецы на различные съезды и конференции, чтобы поразить других светочем мудрости своей.
В конференции участвовали 100 мудрецов иноземных и местных – химики и алхимики. Каждому был задан вопрос: «Если не считать Вас, то кого больше среди остальных участников – химиков или алхимиков?» Когда спросили 51 участника, и все ответили, что алхимиков больше, опрос прервался. Алхимики всегда лгут, а химики всегда говорят правду. Сколько химиков среди участников?
На другой конференции за круглым столом сидели 12 других мудрецов: астрономы и астрологи. Астрономы всегда говорят правду, а астрологи – не всегда. Сколько астрономов за столом, если каждый из сидевших за столом мог заявить, что один из его соседей – астроном, а другой – астролог?
Переаттестация Совета Мудрецов происходит так: король выстраивает их в колонну по одному и надевает каждому колпак белого или черного цветов. Все мудрецы видят цвета всех колпаков впереди стоящих мудрецов, а цвет своего и всех стоящих сзади не видят. Раз в минуту один из мудрецов должен выкрикнуть один из двух цветов (каждый мудрец выкрикивает цвет один раз). После окончания этого процесса король казнит каждого мудреца, выкрикнувший цвет, отличный от цвета его колпака. Накануне переаттестации все сто членов Совета Мудрецов договорились и придумали, как минимизировать число казненных. Скольким из них гарантировано удастся избежать казни?
Калиф Гарун-аль-Рашид одарил троих придворных астрологов прошедших аттестацию, десятью кошельками. Мудрецы, сев подсчитывать доход, обнаружили, что один из кошельков пуст, во втором лежит одна таньга, в третьем – две, и так далее до десятого, в котором оказалось девять таньга. Гусейн Гуслия взял себе два кошелька. Абдурахман ибн Хоттаб и его брат Омар Юсуф поделили оставшиеся кошельки так, что более заслуженный и умудренный годами Абдурахман получил большую сумму денег. По дороге на Омара Юсуфа напали разбойники и отняли четыре кошелька, так что от подарка калифа осталось лишь 10 таньга. Какие кошельки достались Гусейну Гуслия?

Все прошедшие аттестацию мудрецы получают титул магистерский и вступают в тайное общество магистерское, Орденом называемое, ибо мудрость их бесценна и охране подлежит. Но и тут без собраний, хотя бы и тайных не обойтись.
Все магистры трех Тайных Орденов собрались на встречу. После встречи магистр первого Ордена сказал: «Теперь я знаю в два раза больше магистров, чем вчера». Магистр второго Ордена сказал: «Теперь я знаю в три раза больше магистров, чем вчера». Магистр третьего Ордена сказал: «Теперь я знаю в четыре раза больше магистров, чем вчера». Докажите, что кто-то из магистров обсчитался. Предполагается, что до встречи каждый магистр знал магистров только из своего Орден, а после – всех трех орденов.
Мудрецами не рождаются – мудрецами становятся. И если вы не свернете с пути познания, то и вам уготована участь заслужить почетное звание мудреца в молве народной. Готовы ли вы к этой участи? А к безмолвию народному?
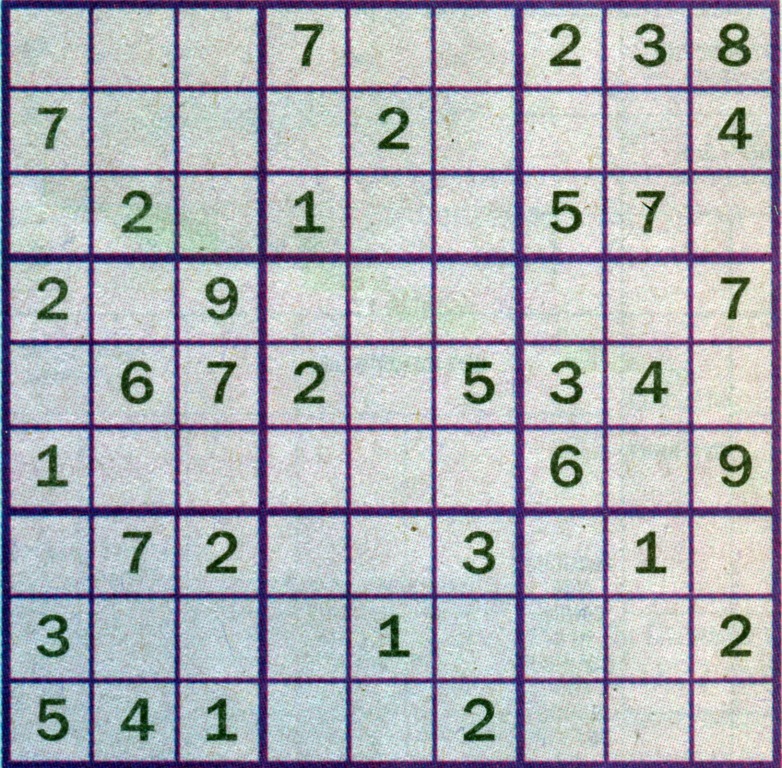
Задание №2: Заполните пустые клетки цифрами от 1 до 9, но так, чтобы в любой строке по горизонтали и по вертикали и в каждом из девяти блоков, отделенных жирными линиями, не было двух одинаковых цифр. Желаем удачи!
8 класс
Задание №1: Ученик должен написать математическое сочинение на заданную тему, в котором он должен дать решение и объяснение поставленных в математическом эссе проблем познания (выделены жирным шрифтом).
Футболисты
Точки зрения на футбол в нашей стране полярные. Порой от ненавистников можно услышать речи о 22 бугаях-бездельниках, которые на потеху таким же бездельникам, сидящим на трибунах, разыгрывают комедию под названием «Футбольный матч». Истинным же ценителям футбола, речи такие неприятны, если не хуже…
Однажды или многократно покоренные этой прекрасной игрой они продолжают ей служить всю оставшуюся жизнь беззаветно, а порой и безответно. Радость от победы любимой команды они выплёскивают на трибунах стадиона, горечь поражений на таких же, как он, болельщиков-горемык. А что в паузах между матчами? – воспоминания о великом прошлом своей команды и мечты о её возрождении уже в следующем туре – нет таким разговорам конца, потому что нет края любви народной к футболу.

Немногие помнят о том, что было в середине прошлого века, а для других это было недавно, почти что вчера… После первого круга в 1967 г. «Динамо» (М) возглавляло турнирную таблицу, «Нефтяник» находился на пятом месте, а «Динамо» (Тб) – как раз посередине между ними. «Динамо» (К) было впереди «Нефтяника», а «Шахтер» занимал место сразу за «Динамо» (Тб). Какая из перечисленных команд находилась на втором месте?
Особенно поражает в таких разговорах умение восстановить в памяти не только положение футбольных команд в турнирной таблице, но и то каких результатов добилась каждая команда в ходе турнира. Может и вы лыком не шиты, и тоже сможете справиться с такой задачей? А может сразу с четырьмя задачами?
Задача первая: В футбольном турнире участвовали пять команд, которые мы будем обозначать по номерам занятых ими мест: А1, А2, А3, А4, А5. Определите, как закончилась каждая игра, если известно, что каждые две команды встречались один раз, причем команда А1 ни разу не сыграла вничью, А2 не проиграла ни одного матча, А4 не выиграла ни одного матча (за победу команда получала 2 очка, за ничью – 1 очко, за поражение – 0 очков).
Задача вторая: В однокруговом футбольном турнире за победу начисляли 3 очка, за ничью 1, а за поражение – 0. Турнир закончился, и очки всех команд были посчитаны. Матч назовем неожиданным, если он завершился победой команды, у которой в итоговой таблице очков меньше, чем у соперника. Могло ли неожиданных игр в турнире быть больше половины?
Задача третья: В коммерческом турнире по футболу участвовало пять команд. Каждая должна была сыграть с каждой ровно один матч. В связи с финансовыми трудностями организаторы некоторые игры отменили. В итоге оказалось. Что все команды набрали различное количество очков и ни одна команда в графе набранных очков не имеет нуля. Какое наименьшее число игр могло быть сыграно в турнире, если за победу начислялось три очка, за ничью – одно, за поражение – ноль?
Задача четвертая: В футбольном турнире участвовали а) 17; б) 16; в) 15 команд. Могло ли случиться, что каждые две команды сыграли один раз и у каждой число её побед равно числу её ничьих?



Победа куется не только на поле. Матч начинается задолго до свистка судьи – с теоретических занятий, на которых разбирается игра противника и разрабатывается тактика успешного противодействия ей на поле для своей команды.
В зале для теоретических занятиях футболистов стоит несколько одинаковых рядов кресел. Если спортсмены попытаются сесть по 6 человек на ряд, то один ряд окажется незаполненным: на него сядут лишь 3 футболиста. Если же футболисты попытаются сесть по 5 человек на ряд, то 4 спортсменам места не хватит. Сколько футболистов и сколько рядов кресел в зале?
Важная фигура на поле – капитан команды. От его деятельности на поле зависит успех в игре команды, в гораздо большей степени, чем от обычного игрока. Поэтому выбор капитана и его заместителя – ответственная и важная задача для каждой команды (11 человек). Сколькими способами это можно сделать?
Все планы на игру останутся только планами, если в футбольную игру вмешается злой рок – болезнь или травма игрока. Тогда необходим новый план – замена игрока не должна ослабить команду, а, наоборот, в идеале, её усилить. Средний возраст 11 игроков футбольной команды – 22 года. Во время матча один игрок получил травму и ушел с поля. Средний возраст оставшихся игроков – 21 год. Сколько лет получившему травму?
Планы на игру строят не только тренера. Каждый болельщик на стадионе – тоже стратег. И если прислушаться к выкрикам с трибуны, то можно сделать вывод, что только болельщикам известен универсальный рецепт победы.
Болельщик Вася нарисовал расположения игроков на футбольном поле к началу первого и второго таймов, чтобы потом проанализировать действия команды после игры. Оказалось, что некоторые игроки поменялись местами, а остальные остались на своих местах. При этом расстояние между любыми двумя игроками не увеличилось. Докажите, что все эти расстояния не изменились.
Большинство экспертов склоняется к тому, что футбол – игра №1 на планете Земля. Поэтому победа или поражение любимой команды сказывается на всем – на производительности труда и на семейной атмосфере. Помните об этом и будьте снисходительны и терпимы к болельщикам в день матча – они идут на встречу с любимой… И вместе с ней они сегодня переживут безграничное счастье от победы или бескрайнюю горечь поражения. Найдите, если в этом есть необходимость, несколько слов поддержки или похвалы, потому что горе и радость болельщика – настоящие!
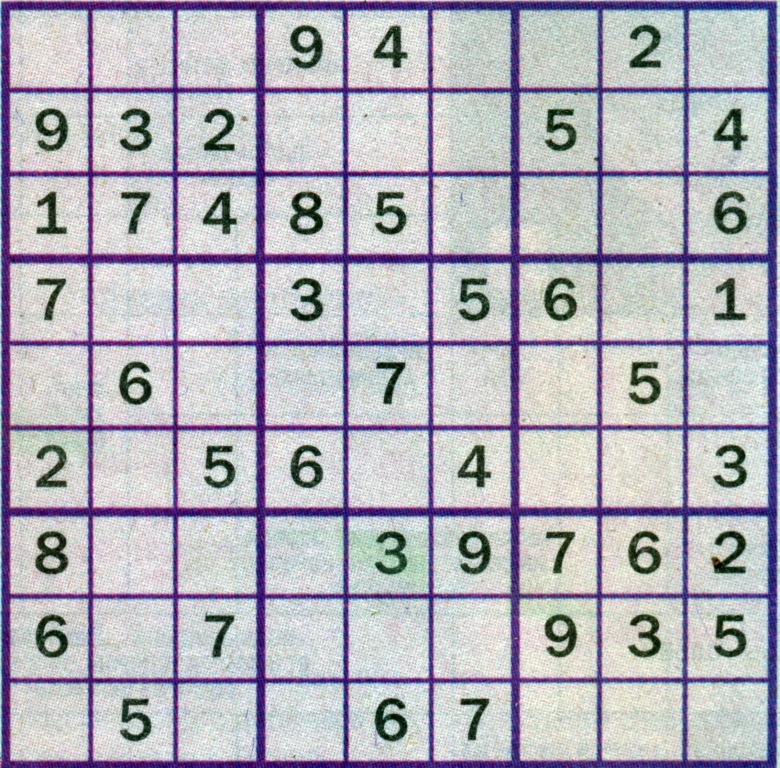
Задание №2: Заполните пустые клетки цифрами от 1 до 9, но так, чтобы в любой строке по горизонтали и по вертикали и в каждом из девяти блоков, отделенных жирными линиями, не было двух одинаковых цифр. Желаем удачи!
9 класс
Задание №1: Ученик должен написать математическое сочинение на заданную тему, в котором он должен дать решение и объяснение поставленных в математическом эссе проблем познания (выделены жирным шрифтом).
Остап Бендер – любимчик богов
Гражданин Остап Бендер отличался от других мошенников, известных человечеству, что знал 400 способов почти законного отъема денег. И один из этих способов – азартные игры.




В черноморском казино Остап Бендер решил сыграть с крупье в фишки. Игра состоит в том, что игроки по очереди (крупье – первым, Остап – вторым) перекладывают фишки с черного поля на красное. За один ход можно переложить не меньше одной фишки и не больше, чем их уже есть на красном поле. Побеждает тот, кто переложил на красное поле последнюю фишку. До начала игры на красном поле лежат 10 фишек, а на черном – некоторое известное Остапу количество (но не ноль). У Остапа в кармане лежат 10 фишек, которые он может до начала игры незаметно подбросить: некоторые - на красное, а некоторые - на черное. Докажите, что он сможет выиграть.
Где же смошенничать не удается, Остап Бендер, терпит фиаско. В Васюках прошли 3 шахматных турнира с одним и тем же составом участников. Известно, что любые два участника сыграли все свои три партии в этих турнирах по-разному: по одному выигрышу, одной ничьей и проигрышу. Остап Бендер набрал меньше всех очков в каждом из первых двух турниров. Какое место он занял в третьем турнире?
После этого Остап Бендер решил дать сеанс одновременной игры Карпову и Каспарову. Один из них должен играть белыми, а другой – черными. Остап уверен, что он или сведет вничью обе партии, или одну выиграет. Как он собирается играть?
Чем же занят Остап Бендер в обычное время? Работает, как и все. Будучи в бытность управдомом, Остап Бендер собирал с жильцов деньги на установку новых квартирных номеров. Адам Козлевич из 105-й квартиры поинтересовался, почему у них во втором подъезде надо собрать денег на 40% больше, чем в первом, хотя квартир там и тут поровну. Не растерявшись, Остап объяснил, что за двухзначные номера приходится платить двое, а за трехзначные – втрое больше, чем за однозначные. Сколько квартир в подъезде?
Для постройки дачи, Остап Бендер приобрел квадратный участок земли и обнес его забором. Что тут криминального, спросите вы? Дело в том, что Остап Бендер получил у доверчивого председателя колхоза документ, в котором сказано, что он имеет право несколько раз произвести следующую операцию: провести прямую через любые две точки забора, огораживающего его участок, снести кусок забора между двумя точками и достроить такой же участок забора с другой стороны симметрично снесенной части относительно выбранной прямой. Сможет ли он такими операциями увеличить площадь своего участка?
Занявшись политической деятельностью, в ходе предвыборной кампании, Остап Бендер организовал в своем городе раздачу слонов населению. На раздачу явилось 28 членов профсоюза местного завода и 37 не членов, причем Остап раздавал слонов поровну всем членам профсоюза и поровну не членам. Оказалось, что существует лишь один способ такой раздачи (так, чтобы раздать всех слонов). Какое наибольшее число слонов могло быть у О. Бендера?
А откуда у Остапа Бендера, такое количество слонов? - Бизнес! Кто не помнит, что им создана компания «Рога и копыта»? За последние годы компания вышла на международный уровень и котируется теперь на всех биржах Европы, Америки и Азии. Курс акций компаний «Рога и копыта» повышается или понижается каждый раз на n процентов, где n – фиксированное целое число, 0 < n < 100 (курс вычисляется с неограниченной точностью). Существует ли n, для которого курс акций может дважды принять одно и тоже значение?
Кто-то скажет, что Остап Бендер – мошенник, а кто назовёт его авантюристом. Но никто не будет отрицать, что Остап Бендер является любимцем народа. Парадокс? – Нет, его любили за то, что он любил жить и жил легко, с улыбкой на устах, встречая поражения, и с достоинством перенося все невзгоды жизни. Нам бы научиться всем этому – цены нам бы не было!
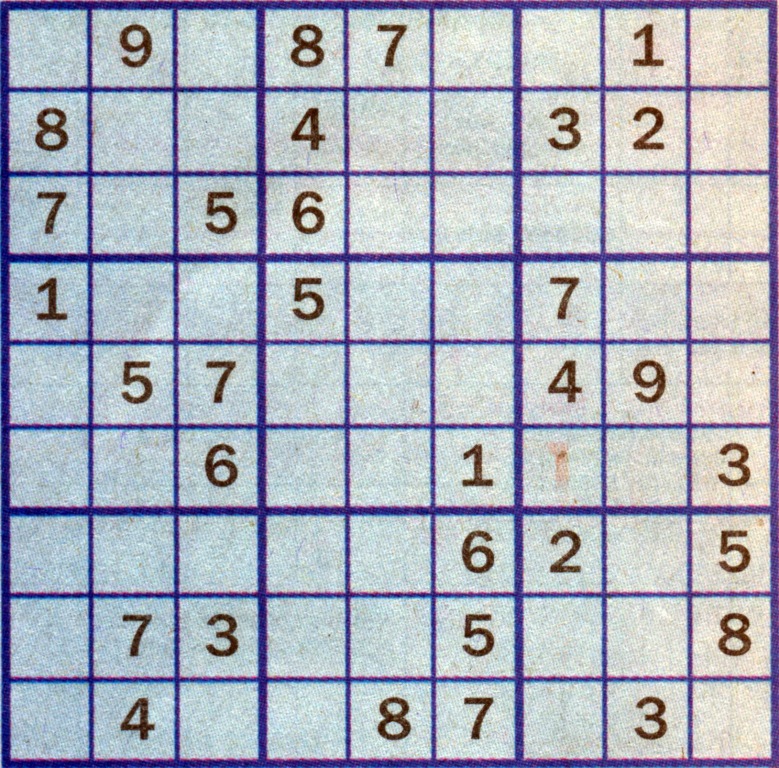
Задание №2: Заполните пустые клетки цифрами от 1 до 9, но так, чтобы в любой строке по горизонтали и по вертикали и в каждом из девяти блоков, отделенных жирными линиями, не было двух одинаковых цифр. Желаем удачи!
10 класс
Задание №1: Ученик должен написать математическое сочинение на заданную тему, в котором он должен дать решение и объяснение поставленных в математическом эссе проблем познания (выделены жирным шрифтом).
Коротышки из Цветочного города
Николаю Николаевичу Носову доподлинно известно, что существует Цветочный город, в котором живут коротышки. Город стоит на реке Огурцовой, названной так из-за произрастающих в городе огромном количестве огурцов. Но не этим известен этот город, а тем, что живут эти коротышки дружно и весело, несмотря на разногласия и причуды жителей Цветочного города.
Конечно, некоего недопонимания между жителями не избежать, ведь они все разные. Это даже отражено в их именах: Знайка и Незнайка, Шпунтик и Винтик, Авоська и Небоська, Пилюлькин, Пончик и Торопыжка. Но договариваться-то надо…
Знайка пришёл в гости к братьям-близнецам Винтику и Шпунтику. Зная, что один из них никогда не говорит правду, Знайка спросил одного из них: «Ты Винтик?» - «Да», - ответил тот. Когда Знайка спросил об этом же второго, то получил столь же чёткий ответ и сразу определил, кто есть кто. Кого из двоих звали Винтиком?
Разногласия редко доходят до ссор, но хоть редко, зато метко… Двадцать пять коротышек делят садовые участки в Цветочном Городе. Каждый участок представляет собой квадрат 1×1, и все участки вместе представляют собой квадрат 5×5. Каждый коротышка находится в ссоре не более чем с тремя другими коротышками. Докажите, что можно распределить участки таким образом, чтобы участки двух поссорившихся коротышек не были бы соседними. (Соседними называются участки, имеющую общую сторону.)
Ссоры коротышек редки, поэтому в Цветочном городе практически повсеместно царит мир и лад. В Цветочном городе живут 2000 коротышек. Каждый коротышка каждый день дарит подарок каждому своему другу. Во избежание разорения, дареное разрешается дарить дальше, но только не тому, кто тебе этот подарок подарил. Знайка посчитал, что никакой из подарков, который подарили любому коротышке в пятницу, не может вернуться к этому коротышке раньше чем в следующую пятницу. Докажите, что у какого-то коротышки не более 12 друзей.
Цветочный город находится на Земле, поэтому все беды и невзгоды, которые переживают земляне не проходят мимо Цветочного города. Коротышки, проживающие в Цветочном городе, вдруг, как и все на планете Земля, стали болеть гриппом. В один день несколько коротышек простудились и заболели, и хотя потом уже никто не простужался, здоровые коротышки заболевали, навещая своих больных друзей. Известно, что каждый коротышка болеет гриппом ровно день, причем после этого у него по крайней мере ещё один день есть иммунитет – т. е. он здоров и заболеть опять в этот день не может. Несмотря на эпидемию, каждый здоровый коротышка ежедневно навещает всех своих больных друзей. Когда началась эпидемия, коротышки забыли о прививках и не делают их. Докажите, что: а) если до первого дня эпидемии какие-нибудь коротышки сделали прививку и имели в первый день иммунитет, то эпидемия может продолжаться сколь угодно долго; б) если же в первый день иммунитета ни у кого не было, то эпидемия рано или поздно кончится.
Чтобы решить все проблемы Цветочного города нужно договариваться, а если договариваться не удается, то тогда нужны демократические выборы. У каждого из жителей Цветочного города знакомые составляют не менее 30% населения города. Коротышка идет на выборы, если баллотируется хотя бы один из его знакомых. Докажите, что можно так провести выборы мэра Цветочного города из двух кандидатов, что в них примет участие не менее половины жителей.
После выборов, победившая партия, начинает переименовывать улицы. В городе Цветочном n площадей и m улиц (m ≥ n+1). Каждая улица соединяет две площади и не проходит через другие площади. По существующей в городе традиции улица может называться либо синей, либо красной. Ежегодно в городе происходит переименование: выбирается площадь и переименовываются все выходящие из неё улицы. Докажите, что вначале можно назвать улицы так, что переименованиями нельзя добиться одинаковых названий у всех улиц города.
Если вы хотите узнать поподробнее о жизни коротышек из Цветочного города, обращайтесь к единственному жителю России, который побывал у них – зовут его Николай Николаевич Носов. Он описал повседневную жизнь жителей Цветочного города и те приключения, которые коротышки пережили не столь давно. Или давным-давно… Это не важно, потому что они молоды и жизнерадостны как всегда, как молоды их читатели и почитатели.
Задание №2: Заполните пустые клетки цифрами от 1 до 9, но так, чтобы в любой строке по горизонтали и по вертикали и в каждом из девяти блоков, отделенных жирными линиями, не было двух одинаковых цифр. Желаем удачи!
11 класс
Задание №1: Ученик должен написать математическое сочинение на заданную тему, в котором он должен дать решение и объяснение поставленных в математическом эссе проблем познания (выделены жирным шрифтом).
Транспортные проблемы современных городов
Автомобильные пробки – беда больших городов. Они неизбежны, как неизбежны день и ночь. Водители оказываются с завидной регулярностью в пробке ранним утром, в полдень и поздним вечером. В каждой стране эту проблему решают по-своему.
В Мехико для ограничения транспортного потока для каждой частной машины устанавливаются два дня недели, в которые она не может выезжать на улицы города. Семье требуется каждый день иметь в распоряжении не менее 10 машин. Каким наименьшим количеством машин может обойтись семья, если её члены могут сами выбирать запрещенные дни для своих автомобилей?
В других странах, таких как Россия, совершенствуют систему общественного транспорта, чтобы максимально удовлетворить потребности горожан не высокого достатка, а также для того чтобы убрать с улиц излишнее количество легковых автомашин. Автобусная сеть такого города устроена следующим образом:
а) с любой остановки на любую другую остановку можно попасть без пересадки;
б) для любой пары маршрутов найдётся, и притом единственная, остановка, на которой можно пересесть с одного маршрута на другой;
в) на каждом маршруте ровно три остановки.
Сколько автобусных маршрутов в городе?
Общественный транспорт не панацея, а всего лишь один из способов избежать транспортного коллапса. В час пик в автобусах не протолкнуться. Что больше: процент переполненных автобусов или процент пассажиров, едущих в переполненных автобусах? (Автобус переполнен, если в нем больше 50 пассажиров.)
Главная проблема общественного транспорта не в его переполненности, а в нерегулярности и непредсказуемости движения общественного транспорта. Вот и приходится решать стоя на остановках головоломки подкидываемые жизнью. Чтобы от театра доехать до цирка, можно сесть на остановке на автобус №1 или на автобус №2. Они ходят с постоянными интервалами, причем автобус №1 в два раза реже, чем №2. За последние 20 минут автобус прошел 16 минут назад, 10 минут назад и 2 минуты назад. Через сколько минут придет следующий автобус?
Можно воспользоваться и такси, но всегда ли это целесообразно? Может надо быть гибче?
Из пункта А в другие можно попасть двумя способами:
а) Выйти сразу и идти пешком.
б) Вызвав машину и, подождав её определённое время, ехать на ней.
В каждом случае используется способ передвижения, требующий меньшего времени. При этом оказывается, что если конечный пункт отстоит на 1 км, то понадобится на дорогу 10 мин, если находится на расстояние 2 км, то 15 мин, если до конечного пункта расстояние 3 км, то для того чтобы добраться до него уже потребуется 17,5 мин. Скорость пешехода и машины, а также время ожидания машины принимаются неизменными. Сколько понадобится времени для достижения пункта, отстоящего от А на 6 км?
Следующий вариант решения проблемы автомобильных пробок связан с тем, что совершенствуется маршрутная сеть и логистика перемещения автомобилей по улицам города, чтобы максимально разгрузить улицы от них самих.
Город устроен по плану, изображенному на рисунке. Из точек А и В одновременно выезжают в одном направлении две машины, которые двигаются с одинаковой скоростью. Доехав до перекрестка, каждая машина или продолжает движение в том же направлении, или поворачивает на 1200 вправо или влево от направления движения (см. рис.). Могут ли машины встретиться?
Города будущего будут не похожи на наши современные города, а тем более на средневековые, с их узкими улочками, где и людям не всегда легко и удобно разминуться. В этих городах, скорее всего, будет найдено решение транспортной проблемы. Но кто может предсказать, какие проблемы возникнут в городах будущего? Никто! На это ответ даст само будущее.
Задание №2: Заполните пустые клетки цифрами от 1 до 9, но так, чтобы в любой строке по горизонтали и по вертикали и в каждом из девяти блоков, отделенных жирными линиями, не